The transformer layer is currently the primary component in natural language processing, playing a leading role in recent innovations such as BERT and GPT-3. Each transformer layer consists of a self-attention sublayer (s) followed by a feedforward sublayer (f), creating an interleaving pattern of self-attention and feedforward sublayers throughout a multilayer transformer model.

Is this interleaved pattern the best way to order these sublayers?

In this post, I’ll explain how we recently found a better way to order these sublayers. That ordering leads to superior performance on multiple language modeling benchmarks.

We started by generating random transformer models, varying the number of each type of sublayer, and their ordering, while keeping the overall model size (number of parameters) constant. Here are a few of these randomly generated models:

(Note that one self-attention sublayer has half the parameters of a feedforward sublayer, so you’ll notice that models that have more feedforward sublayers are shallower. )

We trained these models on the standard WikiText-103 word-level language modeling benchmark. While most of these randomly generated models performed worse than the interleaved model, about a third of these random models outperformed it (mostly by a small margin). Our analysis shows that models with more self-attention toward the bottom and more feedforward sublayers toward the top tend to perform better in general:

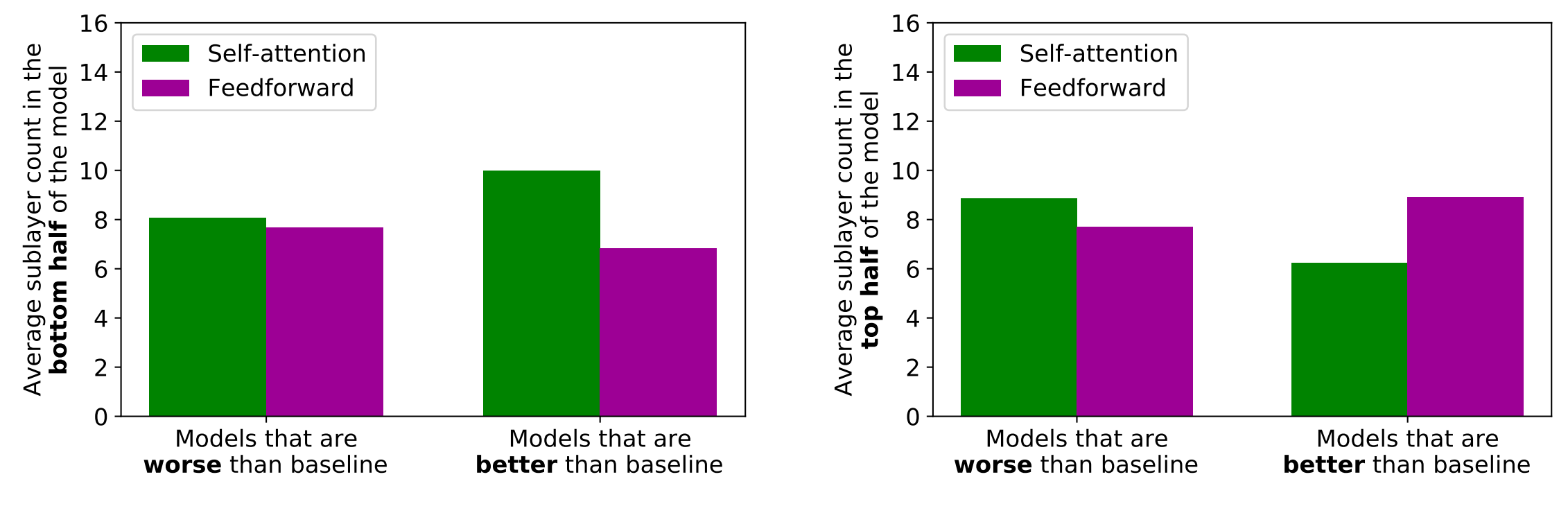
We also observed that models that had an equal number of self-attention and feedforward sublayers tended to perform better than models that had an unequal number of self-attention and feedforward sublayers. Based on this insight, we design a new family of transformer models that follow a distinct sublayer ordering pattern: sandwich transformers. Sandwich transformers are made up of n self-attention sublayers, followed by the regular interleaved transformer pattern, followed by n feedforward sublayers:

Our experiments demonstrate that a sandwich transformer outperforms the baseline interleaved transformer model. This result is made more interesting by the fact that our sandwich transformer is simply a reordering of the sublayers in the baseline model, and does not require more parameters, memory, or training time. On WikiText-103, sandwich transforms improve perplexity while also reducing the variance caused by selecting different random seeds:

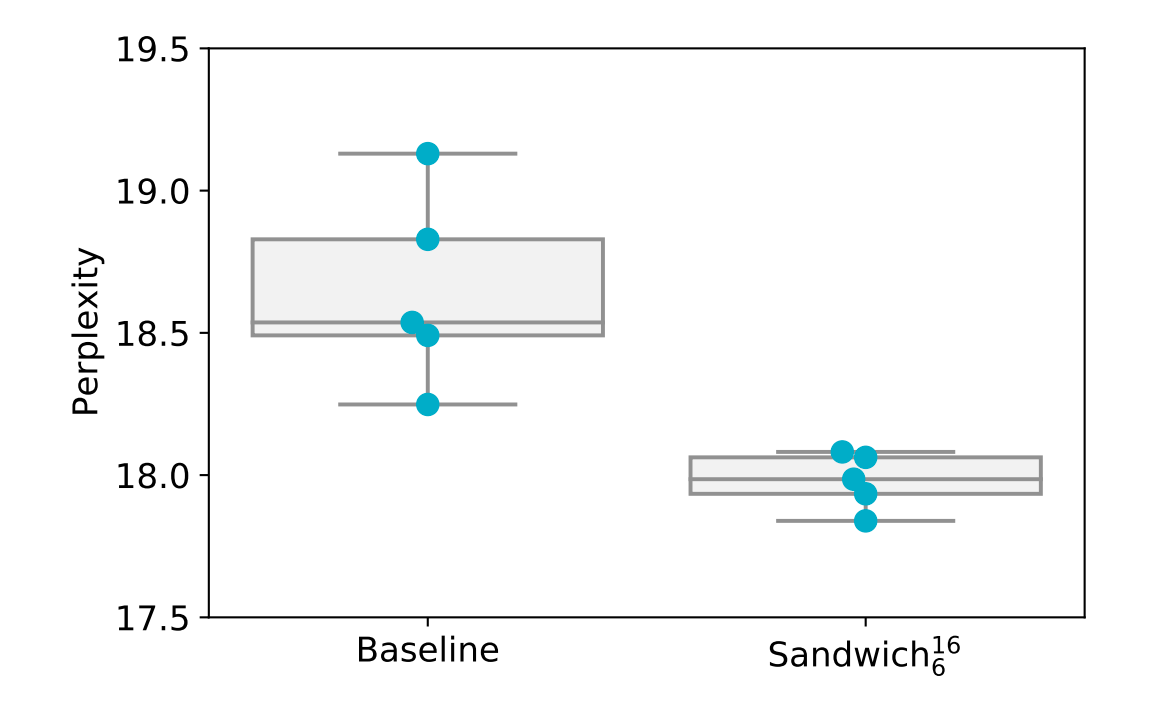
Finally, we demonstrate that even though the sandwich transformer is motivated by random search experiments on WikiText-103, it can improve performance on additional domains and tasks. Sandwich transformers achieve state-of-the-art results on the enwik8 character-level language modeling dataset and on an additional word-level corpus. We conjecture that tuning transformer reorderings to specific tasks could yield even larger gains, and that further exploration of the ordering space may provide universally beneficial patterns.

Other conclusions and insights:

• The transformer layer is not the smallest indivisible unit. The self-attention or feedforward sublayers can each function independently.
• The transformer architecture is quite robust to sublayer order changes. A non-insignificant amount of the random orderings that we trained performed just as well (and sometimes better than) the baseline.
• The ‘extreme standwich’ ordering s¹⁶f¹⁶ (shown below) works almost as well as the baseline on WikiText-103.

• The optimal transformer ordering is not identical across different datasets. For example, the best sandwiching coefficient for WikiText-103 is 6, but the best coefficient for the Toronto Book Corpus language modeling dataset is 7. For character level language modeling the optimal sandwiching coefficients were also different.

The paper is available here. We also have a video presentation available here.